Batch normalization 논문으로 거의 5만회에 가깝게 인용되었다.
배치 놈에 대한 이해는 혁펜하임님의 유툽 영상을 보면 쉽게 이해가 된다. 최고!
딥러닝 모델을 학습할 때 각 층의 입력 분포(파라미터)가 매번 바뀌기 때문에 어려움이 있었다. LR을 낮추게 되어 학습 속도를 늦추게 되고 기울기가 saturation 되는 문제 때문에 초기 값을 설정하는데 과하게 어려운 문제가 있었다. (기울기가 너무 낮으면 전달되는 값이 급격히 작아지므로) 저자들은 이 문제를 internal covariate shift라 하고 미니배치 단위로 들어가는 layer 입력을 정규화(normalize)하여 해결하고자 하였다.
이 방법(BN)으로 LR을 크게 설정하고 초기 입력값도 크게 신경쓰지 않아도 되었다. 실험결과 14배 빠르게 학습을 완료하였다. ImageNet 분류에서도 SOTA를 달성하였다.
SGD에서 데이터셋은 N개로 이뤄져있다. 파라미터의 loss를 최소화 하는 방향으로 학습이 진행된다.

SGD를 학습할 때 초기 값(initial value)을 어떻게 설정하느냐가 중요하다.
미니배치 학습시에 각 층을 지날수록 입력의 분포에 변화가 커지게 되는 문제가 있다(internal covariate shift). 딥러닝 모델을 학습시킬 때 전체 데이터를 한번에 학습시킨다면 데이터의 분포를 정확하게 이해할 것이다. 그러나 예를들어 미니배치로 100번 나눠서 한번 학습시키는 경우에는 100번의 미니배치 샘플이 실제 데이터의 분포와 약간씩 다르기 때문에 학습에 부작용이 있는 것이다.
이를 해결하는 경우 어떤 장점이 있을까?
활성화 함수로 sigmoid를 사용하는 경우를 보면 입력(x)의 절대 값 크기가 크다면 미분은 0에 가깝게 된다. 입력의 절대값이 0에 가까운 경우가 아니라면 기울기가 소실되어(vanishing gradient) 학습이 제대로 되지 않는다. 즉 이를 해결한다면 더 빠른속도로 더 깊은 모델을 학습시킬 수 있다. ReLU 혹은 초기값 설정, 배치 입력의 분포를 안정화(BN)로 해결할 수 있다.


ReLU는 음수는 0으로 양수는 1로 미분값을 출력하는데 만약 입력 값이 전부 양수 영역에 분포한다면 비선형적(non linear)인 관계를 포착하지 못한다. 신경망의 장점은 선형적인 함수로 풀 수 없는 복잡한 분류 문제를 푸는 데에 있기 때문에 ReLU를 사용하던 sigmoid를 사용하던 BN을 사용하면 적절히 값들이 분포되도록 정규화(normalize)하여 선형과 비선형의(non linearlity) 최적점 혹은 전달할 값과 전달하지 않을 값의 최적점을 학습하여 찾는 것이다.
layer normalization은 배치와 상관 없다. 레이어 당 a, b 파라미터 추가, training, test 때 똑같은 방식으로 계산, 배치 크기에 영향을 받지 않는다. BN은 이미지 데이터에 자연어 처리에는 LN을 더 많이 이용한다. BN은 배치별로 분포를 확인해야하는데 자연어 처리 태스크에서는 문장의 길이가 다르기 때문에 긴 문장을 학습할 때 즈음에는 <pad>에 편향적으로 학습하게 된다.
미니 배치에서 BN을 계산하는 방법은 아래 그림과 같다. 입실론은 분모가 0이 되는 경우를 방지하기 위해 추가한다. 혁펜하임님은 아래 식에 따라 nomalize하는 과정을 간단하게 예를들었다. 크기가 5인 배치라고 예를들면 5개의 데이터를 활성화 함수에 뿌린다고 생각하는 것이다. BN은 데이터의 분포가 이상하게 뿌려져 있다면 이를 평균과 분산에 맞도록 잘 뿌리는 과정인 것이다. 감마, 베타 값은 0과 1에 초기화시킨 후 loss를 감소시키는 방향으로 학습된다고 한다.

테스트 시에는 배치의 평균, 배치의 분산의 평균들을 이용한다. 실제 값을 추론(inference)하는 과정에서는 값이 배치 단위로 들어오지 않기 때문에 학습시에 알아낸 미니배치의 평균과 분산으로 모분산을 계산하는 것이다. 분산을 보정하기 위해 m/m-1을 곱한다. 이터레이션을 돌면서 평균을 구해나가는 moving average를 사용한다. (통계학 시간에 배운 내용인데 이렇게 적용이 되는구먼. 논문에서 내용이 나오지만 혁펜하임님 강의를 보고 이해했다...)
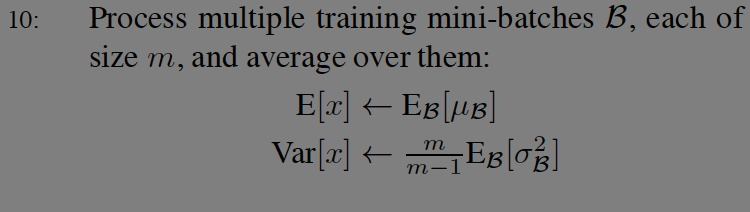
그리고 논문에 의하면 BN을 사용하면 높은 learning rate를 사용해도 된다고 한다. 나머지 실험 부분은 논문 원문을 참고하면 된다.
** 추가로 MLP구조가 아닌 CNN과 RNN에 적용하는 방법에 대해서 이해가 필요하다.
RNN에서 배치놈 적용이 어렵기 때문에 레이어놈이 등장했지만, stack overflow에 검색해보면 다른 방식의 구조에 대한 연구가 있긴 한듯하다. CNN에서는 파이토치의 경우 채널 단위로 평균과 분산 그리고 학습파라미터가 계산이 된다고 한다.
Reference
https://arxiv.org/abs/1502.03167
https://www.youtube.com/watch?v=m61OSJfxL0U (유투브 혁펜하임 강의 BN1)
https://www.youtube.com/watch?v=daDQUBTISVg(유투브 혁펜하임 강의 BN2, LN 포함)
https://youtu.be/SBqpLVE27Is?si=5YfrUi9AmQOtUUGn
'papers' 카테고리의 다른 글
| End-To-End Momory Networks (1) | 2023.11.17 |
|---|---|
| Fast R-CNN (0) | 2023.10.15 |
| Nationality Classification Using Name Embeddings (0) | 2023.09.09 |
| Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling (0) | 2023.07.16 |
| Visualizing and Understanding Convolutional Networks (0) | 2023.05.01 |



